Mogan Gh.L., Butilă E.V., Buzdugan I.D. Proiectarea reductoarelor conico-cilindrice. Universitatea Transilvania din Braşov

Subcap.14.1 Verificarea rulmenţilor radial-axiali cu role conice montaţi pe arborele intermediar

1. SCHEME DE ÎNCĂRCARE

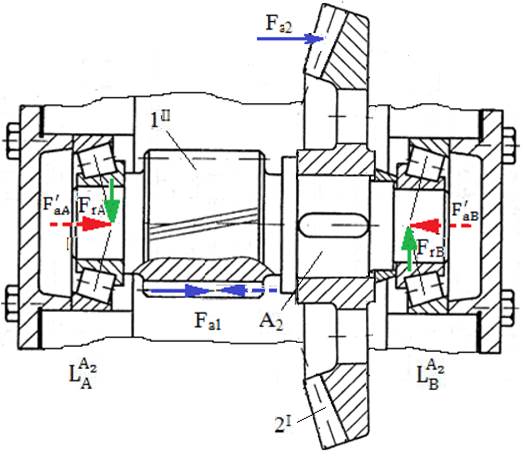
Schema de încărcare a rulmenţilor radial-axiali cu role conice ai arborelui intermediar

2. DATE DE INTRARE

Forţele exterioare

- radiale: F_rA, F_rB (Ex.13.1.1 sau Ex.13.1.2)

- axiale: ±F_a1, F_a2 (Ex.7.2); forţa F_a1 în funcţie de sensul de rotaţie poate avea semnul + (de la stânga la dreapta) sau – (de la dreapta la stâmga) şi deci în funcţie de acestea se impune studiul în 2 cazuri.

Tipul rulmentului şi sarcina (capacitatea) dinamică de bază

Rulment radial-axial cu role conice cu sarcina dinamică de bază C, din catalog pentru rulmenţi (Ex.4.3 sau Anexa.4.3.1.3).

Factorii de influenţă pentru calcul

Valorile factorilor de influenţă e şi Y sunt specifice rulmentului radial-axial cu role (Anexa.4.3.1.3).

Obs. Valoarea maximă a sarcinii dinamice echivalente indică rulmentul cel mai încărcat.

Turaţia arborelui

Rulmenţii se rotesc cu turaţia arborelui intermediar, n = n₂, în rot/min (Ex.2.2).

Durata de funcţionare,

Durata de funcţionare a rulmenţilor este egală cu cea impusă RConCil, L_{h imp} (Ex.1.2.2).

3. SARCINA DINAMICĂ ECHIVALENTĂ MAXIMĂ (RULMENTUL CEL MAI ÎNCĂRCAT) (Calc.0)

Forţele axiale interioare

- din rulmentul lagărului , = 0,5 ;

- din rulmentul lagărului , = 0,5 .

Determinarea încărcărilor axiale a rulmenţilor

Forţa axială totală de încărcare a arborelui intermediar,

F_at = ± F_a1 + - (cazul 1: F_a1 cu semnul + de la stânga la dreapta; cazul 2: F_a1 cu semnul - F_a1 de la dreapta la stânga); F_a2 nu se ia în considerare deoarece se transmite direct la rulmentul din dreapta prin distanţier.

Forţele axiale exterioare din rulmenţi

În funcţie de valoarea forţei axiale totale F_at sunt posibile 3 situaţii:

a. F_at > 0, indică că această forţă are acelaşi sens cu F_a2 şi rulmentul din lagărul este încărcat axial exterior cu forţa, F_aB = F_a2 ± F_a1 + ; rulmentul din lagărul nu este încărcat axial exterior, F_aA = 0.

b. F_at < 0, indică că această forţă are sens opus cu F_a2 şi rulmentul din lagărul este încărcat axial exterior cu forţa F_aA = F_a1 + ; rulmentul din lagărul nu este încărcat axial exterior, F_aB = F_a2.

c. F_at = 0, indică că rulmenţii din lagărele şi nu sunt încărcaţi axial (caz foarte rar) şi F_aA = F_aB = 0.

Determinarea sarcinilor dinamice echivalente (pentru cei doi rulmenţi)

Dacă, F_a = 0,

P = F_r,

iar, dacă F_a > 0 şi

≤ e,

P = F_r + 1,12 Y F_a,

sau

> e,

P = 0,67F_r + 1,68 Y F_a,

unde, valorile factorilor de influenţă e şi Y sunt specifice rulmentului radial-axial cu role (Anexa.4.3.1.3).

Obs. Valoarea maximă a sarcinii dinamice echivalente indică rulmentul cel mai încărcat.

4. VERRIFICAREA RULMENTULUI CEL MAI ÎNCĂRCAT (Calc.0)

Determinara durabilităţii rulmentului cel mai încărcat

L = [milioane de rotaţii],

unde, exponentul durabilităţii p = 10/3 (pentru rulmenţi cu role).

Determinara duratei de funcţionare a rulmentului cel mai încărcat

L_h = [ore].

Verificarea duratei de funcţionare a rulmentului cel mai încărcat

Situaţii posibile:

a. L_h < L_{h imp}, rulmentul nu rezistă fără să deterioreze numărul de ore impus şi se impune realegerea altui rulment de acelaşi tip (radial-axial cu role conice, Anexa.4.3.1.3), de preferat cu acelaşi diametru interior (d), dar cu seria de dimensiuni mai mare care are sarcina dinamică de bază mai mare.

b. L_h > (1…≈1,5) L_{h imp}, rulmentul este corespunzător.

c. L_h > ≈1,5 L_{h imp}, rulmentul este supradimensionat (componentele active ale RConCil se deteriorează cu mult înaintea rulmentului cel mai încărcat) şi se poate realege un alt rulment de acelaşi tip (radial-axial cu role conice, Anexa.4.3.1.3), de preferat cu acelaşi diametru interior (d), dar cu seria de dimensiuni mai mică care are sarcina dinamică de bază mai mică.

Obs. În cazul realegerii rulmentului se impune:

- reverificarea acestuia pornind cu calculul sarcinii dinamice echivalente urmat de determinarea durabilităţii şi duratei de funcţionare.

- modifica modelelor 3D (CATIA) ale rulmentului şi carcaselor ţinând cont de noile dimensiuni ale acestuia